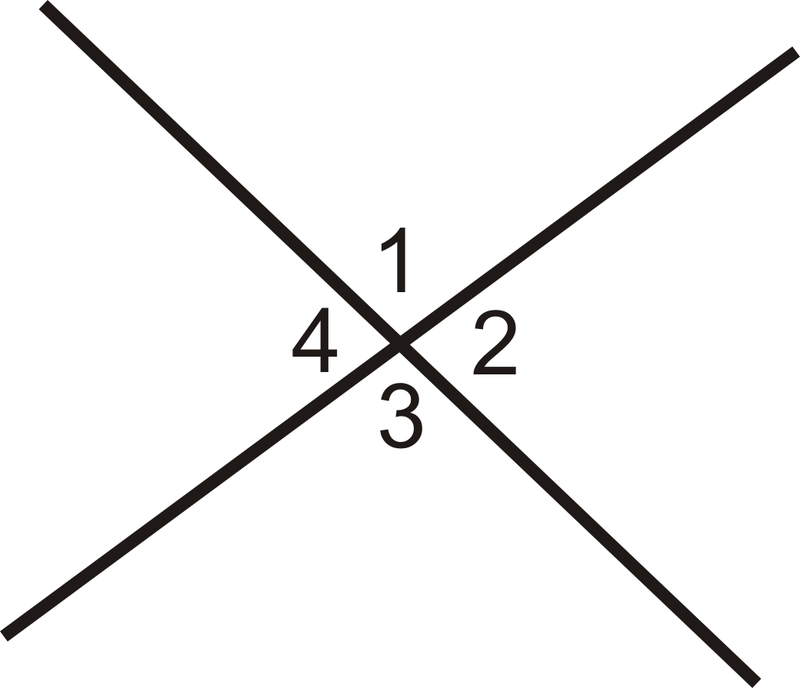
Have you heard about the term ‘angles’?. No! Let me tell you when two vertical or horizontal lines meet each other at a common point an angle is formed. There are various types of angles such as acute angle, right angle, reflex angle, and so on. Similarly, vertical angles are a type of angle that is always equal and is formed by the intersection of a point. When two different angles are opposite to each other, vertical angles are formed. These angles are also known as the vertically opposite angles. In this article, we will try to cover various aspects related to vertically opposite angles such as congruent angles, important notes or properties of vertical angles, and so on and do a detailed analysis about them.
Congruent Angle
A type of angle that is generally seen in some triangles like an equilateral triangle, the isosceles triangle can be defined as the congruent angle. It can also be defined as the angles where the measure of two angles is exactly the same. A lot of theorems are based on the congruent angle such as corresponding theorem, vertical angle theorem, congruent supplement, complement theorem, and many more. These theorems can be used to satisfy the theorem of congruent angles. The literal meaning of ‘congruent’ shapes having similar sizes and angles. In the next few topics, we shall learn about the construction of congruent angles in terms of measurement.
Theorem and Proof of Vertical Angle
The theorem of the vertical opposite or vertical angles defines that two angles which are opposite, also known as vertical opposite angles, are always equal when intersected. The vertical opposite angles are also congruent ( similar size and angle ). To prove the theorem of vertical angles, a straight angle is used which basically measures 180 degrees. The following points below analyses the steps to prove a theorem of vertical angles;
- Whenever you prove a theorem about vertically opposite angles, you may need a figure where angle 1 + angle 2 is equivalent to 180 degrees. Similarly, angle 1 + angle 4 is also equivalent to 180 degrees.
- All of these angles are linear pairs, thus they measure about 180 degrees. The transitive property of angles define that, a = b and a = c and b =c. Thus, from this property we can say that, angle 1 + angle 2 = angle 1 + angle 4 ( 180 = 180).
- Now, if we eliminate angle 1 from both the equations, we may get angle 2 is equivalent to angle 4. Likewise, if we do the vice-versa, angle 3 = angle 1.
- Thus, angle 1 = 2 = 3 = 4 which signifies that the vertically opposite angles are always equal to each other. In order to find the measurement of the angles, we use the theorem of vertically opposite angles.
Steps of Constructing a Congruent Angle
Till now, you may have underwood about the angles and their types such as congruent angle and vertical angle. The congruent angle is defined as the angles where the measure of two angles is exactly the same. In the next few points, we will discuss the construction of congruent angles.
- Draw a straight line that is horizontal with a rule of any unit. Name them A and B.
- Make an arc with the help of your compass. The arc should be smaller than the line made previously. Name the arc as ‘D’.
- Now make a separate arc and name it as ‘C’.
- Join the horizontal line of ‘A’ with the arc made separately ‘C’. Your congruent angle has been formed.
- Similarly, you can form a different angle with the help of the above methods.
Visit the website of Cuemath if you want to learn about these topics more and book a free session.
